ST表

最近刷题有点疯狂，写篇ST表冷静一下，顺便回顾一下。

什么是ST表

傻子或大犇都会看的定义

ST表是一种用于解决区间最值问题的数据结构，它的全称是Sparse Table，意为稀疏表。它的主要思想是预处理出每个区间的最值，然后通过预处理的结果来快速求出任意区间的最值。

有点蒙? 没关系，我当初也是，下面我会十分详细的一步一步推导。

从求最大值说起…

现在有一个序列a，我们想要求出区间$[l,r]$的最大值，请问该怎么做?
想必大家都会想到枚举这一优美且高效(搞笑)的方法，所以我们不妨试一试。

方法自然是从$a[l]$开始枚举到$a[r]$，每两个数取最大值，最后得到的就是区间$[l,r]$的最大值。

int ans = a[l];
for(int i = l + 1; i <= r; i++)
    ans = max(ans, a[i]);

真逝完美!
来分析一下时间复杂度，每次枚举需要$O(1)$，总共需要枚举$r-l+1$次，所以总时间复杂度为$O(n)$。还算过得去，对吧?但是，出题老师不可能放你暴力过的，倘若ta轻描淡写地来一句 “n组询问，每组一个[l,r]“，那就惨了，代码就被迫变成了这样:

int ans = a[l];
for(int i = 1;i <= n;i++)
    int l, r;
    cin >> l >> r;
    for(int j = l;j <= r;j++)
        ans = max(ans, a[j]);

这样的时间复杂度就是$O(n^2)$了，显然是不可接受的。为了解决这个问题，ST表应运而生。

ST表的过程

ST表只有两个步骤，第一个是$O(n\log{n})$的预处理，第二个是$O(1)$的查询。显然比暴力要快得多。

预处理

预处理用到了动态规划的思想，我们定义一个二维数组 $st$ ，其中 $st_{ij}$ 表示从 $a_i$ 开始，长度为 $2^j$ 的区间的最大值。也就是区间$[i,i+2^j-1]$的最大值。

接下来便是构造动态转移方程，在构造之前，先来看看求最大值这件事的一个性质:

$$max(a_1,a_2...a_n)=max(max(a_1,a_2...a_k),max(a_k,a_{k+1}...a_n))$$

这个性质很好理解，就是把一个区间分成两个区间，然后求两个区间的最大值，最后再求两个最大值的最大值，就是整一个大区间的最大值。这样就把一个大区间的最大值转化成了两个小区间的最大值。

这么说……撕，那转移方程不就有了吗?对于$[i,i+2^j-1]$的最大值，就有:

$$max([i,i+2^j-1])=max(max([i,i+2^{j-1}-1]),max([i+2^{j-1},i+2^j-1]))$$

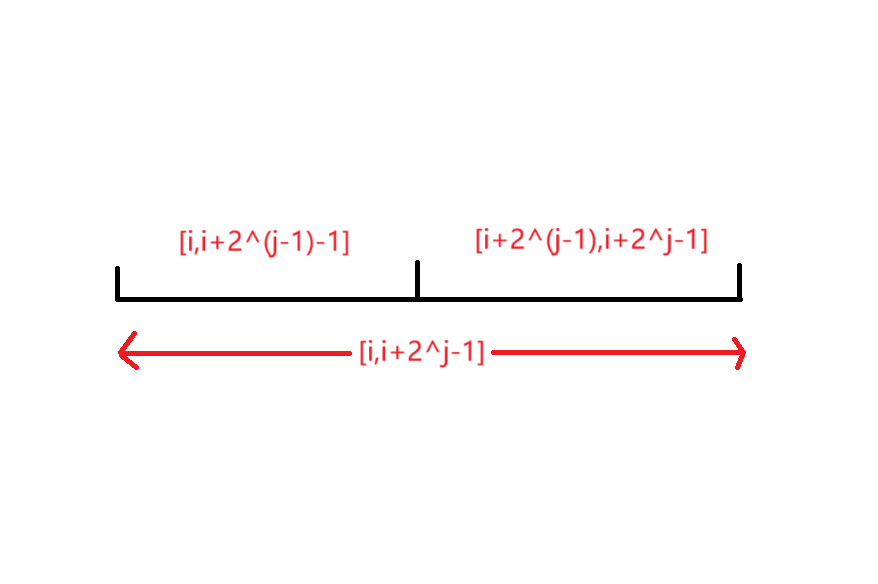
而:

$$max([i,i+2^{j}-1])=st_{i,j}$$ $$max([i,i+2^{j-1}-1])=st_{i,j-1}$$ $$max([i+2^{j-1},i+2^j-1])=st_{i+2^{j-1},j-1}$$

所以:

$$st_{i,j}=max(st_{i,j-1},st_{i+2^{j-1},j-1})$$

这样转移方程不就出来了么?

for(int i = 1;i <= n;i++)//枚举起点
    st[i][0] = a[i];
for(int j = 1;j <= \log2(n);j++)//枚举区间长度
    for(int i = 1;i + (1 << j) - 1 <= n;i++)//枚举起点
        st[i][j] = max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);//(1 << j) = 2^j

查询

查询的时间复杂度度是$O(1)$的。既然我们已经预处理出所有起点的所有长度为$2^j$的区间的最大值，如果我们要查询$max([l,r])$，其实只需要找到这段区间所对应的$st{lx}$就行了。在区间和$st$表中，$l$和$i$的意义都是一样的，所以$i$就是$l$，而$x$也不难推导，我们知道$st{ix}$就是$max([i,i+2^x-1])$，而我们要查询$max([l,r])$，所以

$$r=i+2^x-1$$

因为$i=l$，所以

$$\begin{align} r&=l+2^x-1\\ 2^x&=r-l+1\\ x&=\log(r-l+1) \end{align}$$ 然而真有那么简单吗!

确实

由于$\log$函数的值是浮点数，向下取整可能导致查询的区间长度不够，向上取整又可能多查了，这怎么办?
在预处理的时候提出了一个性质:

$$max(a_1,a_2...a_n)=max(max(a_1,a_2...a_k),max(a_k,a_{k+1}...a_n))$$

把它稍微改一下:

$$max(a_1,a_2...a_n)=max(max(a_1,a_2...a_m),max(a_{k},a_{k+1}...a_n))\\其中，m{\le}n,k{\ge}1$$

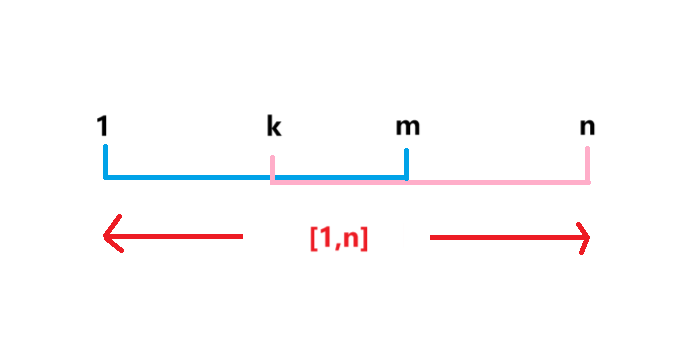
也就是说，就算被拆成的两个区间有重叠，只要它俩能填满整个区间，那么这整个区间的最大值就是这两个区间的最大值的最大值。这样就可以解决上面的问题了，我们只需要对$x=\log(r-l+1)$向下取整，即

$$x=\lfloor \log(r-l+1) \rfloor$$

然后用$r-(2^x-1)$，记为$d$，就是这一段

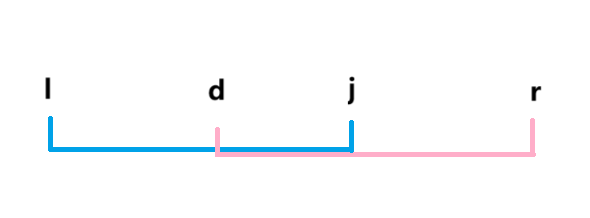
如图3所示，$[l,x]$和$[d,r]$的长度都是$2^x$，所以我们可以直接用$st{lx}$和$st{dr}$来代替$max([l,r])$，也就是

$$max([l,r])=max(st_{lx},st_{dr})\\$$

代码:

int find(int l,int r){
    int x=Log2[r-l+1];
    return max(st[l][x],st[r-(1<<x)+1][x]);
}

小优化

上面的代码还是有点慢，因为$\log$函数是$O(\log{n})$的，所以我们可以用一个数组来存储$\log$函数的值，这样就不用每次都要调用$\log$函数了。

for(int i = 2; i <= n; i++)
    Log2[i] = Log2[i >> 1] + 1;

ST表的应用

通过上面的例子，很容易看出ST表在求最大值的时候的优越性，但是ST表不仅仅可以求最大值，还可以求最小值，甚至是求区间和，区间异或和等等。
其实，这一类问题都被称为可重复贡献问题，定义就是对于运算$opt$,有$x$ $opt$ $x=x$，像$max(x,x)=x，min(x,x)=x$等。

但ST表也有它的不足，比如它只能维护少量信息，而且不支持修改。

几道破题

P3865 【模板】ST表

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+1;
int n,m,st[N][100],Log2[N];

inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
	return x*f;
}

void initST(){
    for(int j=1;j<=21;j++){
        for(int i=1;i+(1<<j)-1<=n;i++){
			st[i][j]=max(st[i][j-1],st[i+(1<<j-1)][j-1]);
        }
    }

}
void initLOG2(){
    for (int i=2;i<=n;i++)
    Log2[i]=Log2[i/2]+1;
}
int find(int l,int r){
    int x=Log2[r-l+1];
    return max(st[l][x],st[r-(1<<x)+1][x]);
}

int main(){ 
	n=read(),m=read();
	
	for(int i=1;i<=n;i++){
	    st[i][0]=read();
	} 
    initST();
    initLOG2();
    for(int i=1;i<=m;i++){
        int l=read(),r=read();
        printf("%d\n",find(l,r));
    }
	
	
	return 0;
} 

没啥好说的，就是模板题，不过这题的数据强度不低，记得用快速读入。

P2880 [USACO07JAN] Balanced Lineup G

#include<bits/stdc++.h>
using namespace std;
const int N=5e4+1;
int n,q,stMax[N][23],stMin[N][23],Log2[N];
void initLOG2(){
	for(int i=2;i<=n;i++)Log2[i]=Log2[i/2]+1;
}
void initST(){
	for(int j=1;j<23;j++){
		for(int i=1;i+(1<<j)-1<=n;i++){
			stMax[i][j]=max(stMax[i][j-1],stMax[i+(1<<j-1)][j-1]);
			stMin[i][j]=min(stMin[i][j-1],stMin[i+(1<<j-1)][j-1]);
		}
	}
}
int find(int l,int r){
	int x=Log2[r-l+1];
	int maxx=max(stMax[l][x],stMax[r-(1<<x)+1][x]);
	int minn=min(stMin[l][x],stMin[r-(1<<x)+1][x]);
	return (maxx-minn);
}
int main(){
	scanf("%d%d",&n,&q);
	for(int i=1;i<=n;i++){
		scanf("%d",&stMax[i][0]);
		stMin[i][0]=stMax[i][0];
	}
	initST();
	initLOG2();
	for(int i=1;i<=q;i++){
		int a,b;
		scanf("%d%d",&a,&b);
		printf("%d\n",find(a,b));
	}
	return 0;
} 

同样没啥好说的，最大值和最小值同时求就好。