将一棵树剖分成若干条链，使得树上的路径转化为链上的路径，从而将树上的问题转化为链上的问题，这就是树链剖分。而重链剖分是树链剖分的其中一种，其不同点在于剖分的方式。

重链剖分剖分方式

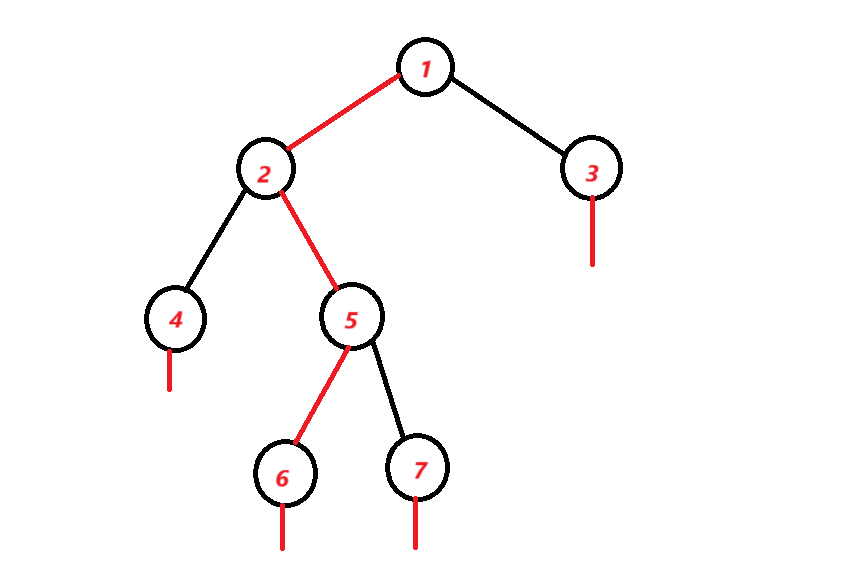
重链剖分的剖分方式是：每次选择子树中最大的子树作为重儿子，其余的子树作为轻儿子。而重链是指一条从根节点到当前节点的路径上，出根节点外，链上其他节点都是重儿子的连边构成的链。如下图：

重剖

图中的红色边就是重链，而黑色边就是轻链。每个叶子节点也有一条以自己为起点，长度为 $0$ 的重链。

从图中还能看出，每个节点至多只能有一个重儿子。

重链剖分的几个重要数组

$de[i]$：编号为 $i$ 节点的深度。

$fa[i]$：编号为 $i$ 节点的父节点。

$hs[i]$：编号为 $i$ 节点的重儿子。

$s[i]$：编号为 $i$ 节点的子树大小。

$dfn[i]$：编号为 $i$ 节点在重链优先遍历序列中的位置。重链优先遍历即先遍历重链，再遍历轻链的遍历方式。这样可以保证在重链上的节点在数组中是连续的，所以可以用线段树等数据结构维护。

$rnk[i]$：重链优先遍历序列中第 $i$ 个节点的编号。$dfn[i]$的下标和值交换的数组。

$top[i]$：编号为 $i$ 节点所在重链的顶端节点。

重链剖分的过程

重链剖分的过程由两个$dfs$完成，第一个$dfs$用于求出每个节点的$de[i]$、$fa[i]$、$s[i]$、$hs[i]$，第二个$dfs$用于求$dfn[i]$、$rnk[i]$、$top[i]$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
const int N=1e5+5;
vector<LLI> t[N];

LLI de[N];
LLI fa[N];
LLI s[N];
LLI hs[N]; 
void dfs1(LLI x,LLI fath){
	fa[x]=fath,de[x]=de[fath]+1,s[x]=1;
	LLI smax=INT_MIN;
	for(LLI i=0;i<t[x].size();++i){
		if(t[x][i]!=fath){
			dfs1(t[x][i],x);
			s[x]+=s[t[x][i]];
			if(smax<s[t[x][i]])
				smax=s[t[x][i]],hs[x]=t[x][i];
		}
	}
}

LLI dfn[N];
LLI rnk[N];
LLI top[N];
LLI cnt;
void dfs2(LLI x,LLI topf){
	dfn[x]=++cnt;
	top[x]=topf;
	if(!hs[x])return;
	dfs2(hs[x],topf);
	for(LLI i=0;i<t[x].size();++i){
		if(t[x][i]!=fa[x]&&t[x][i]!=hs[x])
		dfs2(t[x][i],t[x][i]);
	}
}

重链剖分的应用

重链剖分的应用主要是解决树上的路径问题，如树上两点的最短路径、树上两点的最大值等问题。通过重链剖分，我们可以将树上的问题转化为链上的问题，从而用线段树，树状数组等数据结构解决。

但无论是查询还是修改，都需要去跳重链 我自己都不知道在说啥，比如查找树上两点最短路点权和，如果这两个点在同一条重链上，那么就可以直接用数据结构查询，否则就要不断跳到自己父亲节点的重链链顶并且加上这条重链的点权和，直到两点在一条重链上。

1
2
3
4
5
6
7
8
9
10
11
12
while(top[x]!=top[y]){
	if(de[top[x]]<de[top[y]])swap(x,y);

    //某些操作，比如查询和修改
    //...

	x=fa[top[x]];
}
if(de[x]>de[y])swap(x,y);

//...