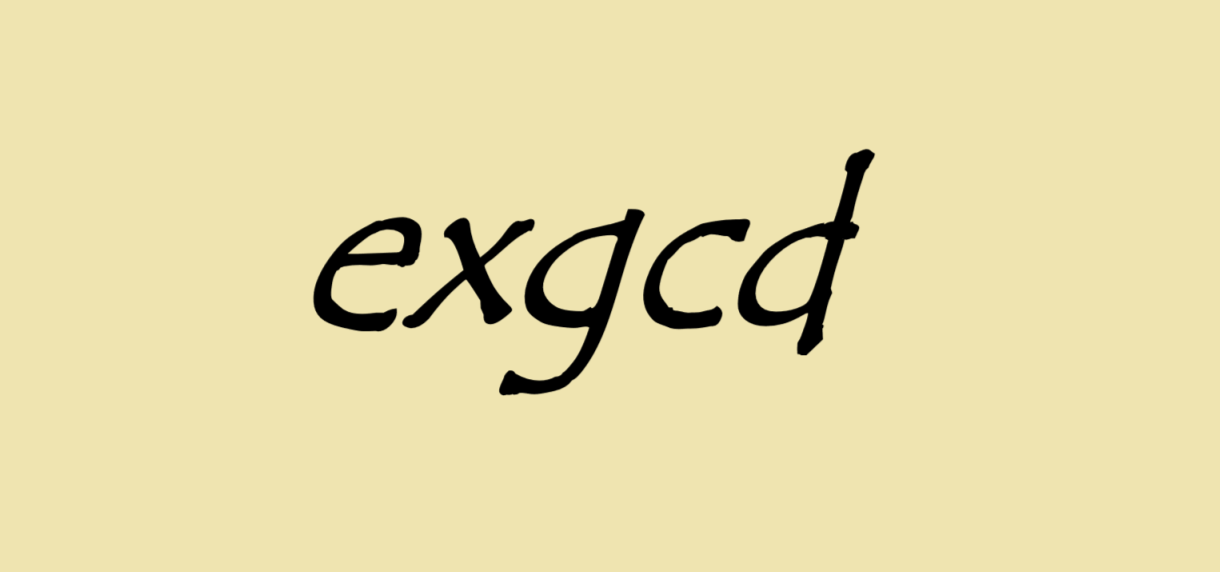最近开始思考起了阶乘加速的问题，深入思考了一下，得到了一些有趣的想法。

尝试1：分治

既然阶乘最朴素的算法都是$O(n)$的，那么最直接的想法就是把$n$踢掉，在塞个$\log{n}$之类进去，自然就是分治了。

想法1

第一个想法是每次从中间切开，分成 $1\times2\times3\times…\times \frac{n}{2}$ 和 $(\frac{n}{2}+1)\times(\frac{n}{2}+2)\times(\frac{n}{2}+3)\times…\times n$ 两部分，然后递归求解。
但这样，子问题的性质好像发生了改变，虽然它俩都是求区间积，但一个是从1开始，而一个是从$\frac{n}{2}+1$开始，并非求阶乘，就让人很难受，所以我立马放弃了这个想法。

其实是我想半天也没想出怎么处理子问题

想法2

第二个想法差点让我相信它就是我想要的答案了，同样是分成两部分，FFT给了我一点启发，这次我把奇数和偶数分成两组：$1\times3\times5\times7\times…$ 和 $2\times4\times6\times8\times…$

先单看偶数部分，你就会发现这太让人高兴了，每个数字提个$2$出来就变成了$2^m(1\times2\times3\times4\times…)$，后半部分又可以递归分解，但坏就坏在奇数部分，这简直折磨死人，我尝试了各种办法想把它处理 (比如把奇数表示成偶数$+1$)，可十分不幸，这些方法都不可行，于是我十分甚至九分不舍地放弃了这个想法。

尝试二：素数

脑子里突然闪出一个想法。

根据唯一分解定理：

其中$p_i$为素数，$e_i$为质数$p_i$的指数。
那么$n\times m$不就是两数分解后对应素数指数相加吗？举个例子，假设

那么

也就是说，即使是 $1\times2\times3\times…\times n$，分解出来也不过是一堆素数，每个素数头上顶个指数罢了！那么这时就有想法了，只要通过某种手段获取到每一个素数的指数，就能使用快速幂来求出素数的对应次方，最后累乘起来就是答案，如果$\pi(n)$表示$[1,n]$中的素数个数，那么时间代价就是。

接下来构造所谓“某种手段”，最后，想到了一种 的方法，方法很简单，我们知道，在 这个序列中，从开始，每隔个数字就有一个能整除$p_i$的数字。假设，在中，都能被整除，总共个数字，把加到对应的指数中，那么这些数字中，有个能被$3^2$整除，再把加到中，以此类推，我们只需要不断将除以，将每次除得的数字加到中，直到为止，这样就能得到的指数$e$了，加上前面所推，总时间复杂度为

但其实这有个缺陷，那就是必须先求出$[1,n]$中的所有素数，这个代价是$O(n)$，但转念一想现实中都是机器先打好素数表，然后再用，所以这个缺陷也不是很大。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
const int N=1001;
int n;
vector<int>primes;
//int primes[N]={2,3,5,7......} 
bool vis[N];
void get_primes(int n){
	for(int i=2;i<=n;i++){
		if(vis[i])continue;
		primes.push_back(i);
		for(int j=i+i;j<=n;j+=i){
			vis[j]=1;
		}
	}
}

long long int fast_pow(int a,int x){
	if(x==0)return 1;
	if(x==1)return a;
	long long int p=pow(a,x>>1);
	return p*p*(x%2?a:1);
}

long long int fast_fac(int n){
	long long int ans=1;
	for(int i=0;i<primes.size();i++){
		long long int e=0,p=primes[i],x=n;
		while(x>=p)e+=(x/=p);
		ans*=fast_pow(p,e);
	}return ans;
}